A Guide to Activation Functions in Artificial Neural Networks

Activation functions are mathematical equations attached to the end of every layer of an artificial (deep) neural network. This helps in computing the output and figuring out if nodes would fire or not. They also help neutral networks learn complex nonlinear relationships in data.
What Does Node’s Firing Mean
The phrase “node will fire or not” is a metaphorical way of describing how a neuron in an artificial neural network processes input signals. In the context of neural networks, a “node” is a computational unit that simulates the behavior of biological neurons. These nodes “fire” when a certain threshold of activation is reached. To elaborate:
In a biological neuron, when the inputs—received through the dendrites from other neurons—accumulate to a certain level of electric potential, the neuron activates and sends an electric spike along its axon to other neurons.
Similarly, in an artificial neural network, a node receives numerical inputs, which are typically weighted sums of outputs from nodes in the previous layer. The role of the activation function is to decide whether this weighted sum is sufficient to activate the node.
When we say that an activation function determines if a “node will fire or not,” we are analogizing this process to its biological counterpart. In practice, for a node in a neural network, “firing” means producing a non-zero output.
If the weighted sum of inputs does not meet a certain threshold—determined by the activation function—the node will not activate and will output a value corresponding to “not firing,” which could be zero or another value depending on the function used.
Activation functions like the sigmoid or ReLU (Rectified Linear Unit) effectively decide whether the signal that a node is processing is significant enough to be passed on to the next network layer. This process is critical in allowing the network to learn complex patterns, as different nodes will be responsible for activating different parts of the network based on the features present in the input data.
Classifications
We can classify neural network activation functions into two categories. These categories are linear and nonlinear activation functions.
Linear activation functions make the layer’s output directly proportional to the product of the input and weights passed into it. Nonlinear activation functions like sigmoid and TanH can learn the complex mapping between inputs and outputs. Unlike linear activation functions with a derivative of 1, we can train it with backpropagation.
Types of Activation Functions
1. Sigmoid Activation Function
At some point, this was the most popular activation function (and I still use it by default at times), but we substituted it for the Tanh function, and we will explain why soon. The sigmoid function maps incoming data between 0 and 1.
The following picture explains the formula and plotting of the sigmoid function:
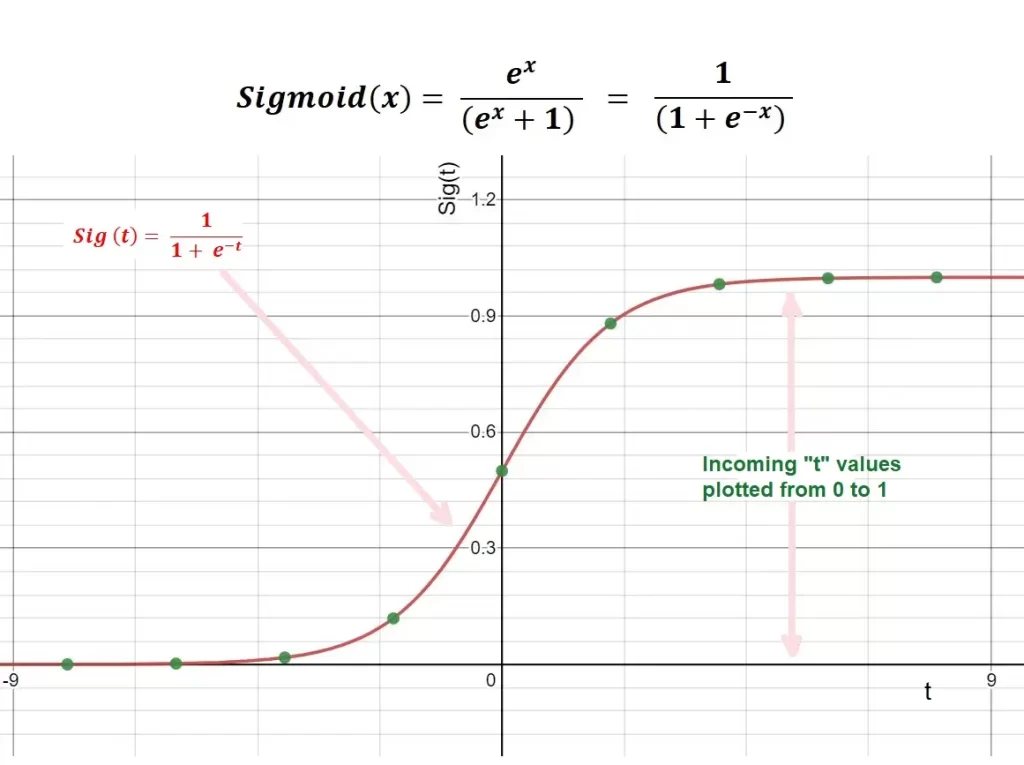
The sigmoid function is still a good way of finding a nonlinear relationship, and it has some major drawbacks that let us opt for other types of activation functions
Cons of Sigmoid Activation Function
Vanishing gradient problem
If we notice, our slope turns to a straight line at 0 and 1. At that point, large changes in the values of inputs would not lead to similar changes in the value of the output of our activation function. This means that weights do not update quickly during backpropagation and can lead to slow convergence.
Not zero centered
Let’s assume you are driving a problematic car that can’t stay in a straight line, meaning a slight change in the steering leads to big sways in the car’s direction. This means that after the ride, we would have had more mileage than we should have had because our car could not move in a straight line.
When we use the sigmoid activation function, all our weight updates are either negative or positive. This is inefficient because, at times, the updates needed for our W1 are negative and for W2 are positive. This causes the value of our loss function to swing in directions towards its arrival at its goal.
This implies that it would take longer for us to reach our goal and, therefore, a longer training time.
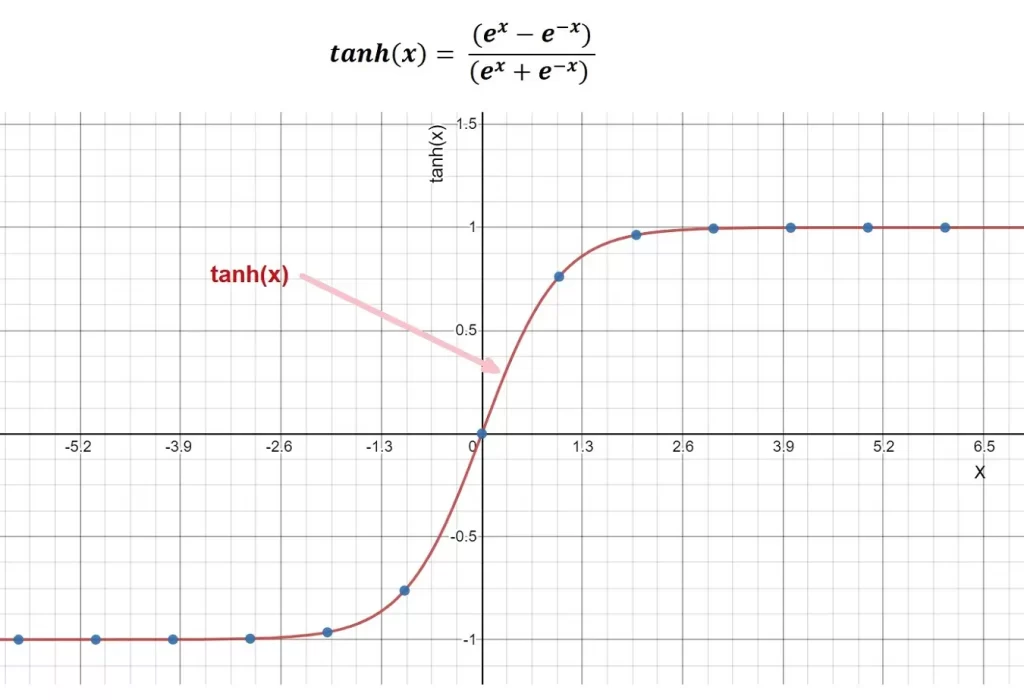
Tanh Activation Function
Tanh is another activation function but very similar to the sigmoid activation function. In Tanh activation function, instead of the range 0 and 1, our values are now skewed to -1 and +1.
The following picture describes the Tanh function:
The Tanh activation function suffers from what our sigmoid function suffers from when values reach the maximum or minimum on the graph, and the derivatives go towards 0 (Zero).
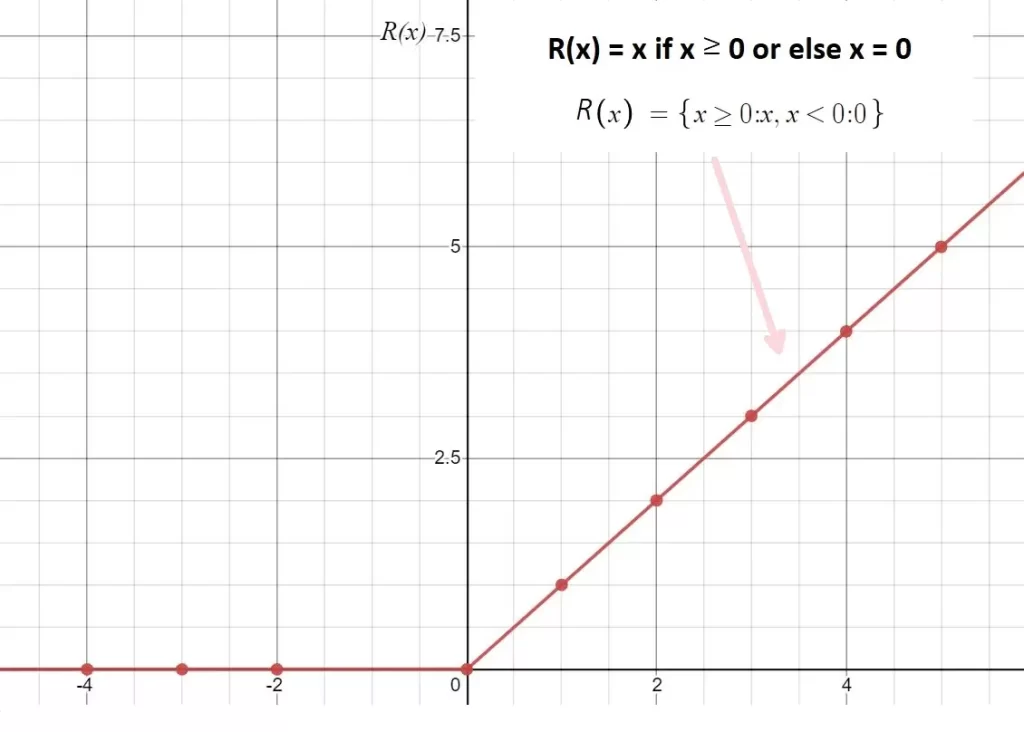
Rectified Linear Unit (ReLU) Activation Function
Rectified Linear Unit of ReLU is one of the most common activation functions currently. It is used in image classification a lot. This is a linear activation function that has a lower threshold of 0 and can be defined as max(0, x)
Pros of ReLU
- The activation function reaches the Global minimum of the loss function better than other activation functions, and this is due to it being linear.
- It is less computationally expensive.
Cons of ReLU
The two main issues or RELU are in the upper and lower boundaries of the function. The easiest to understand is that the upper limit has no boundary, so X can actually reach infinity and beyond, and that would not work for our model.
The second issue is the lower boundary. What it means is that a negative number turns to 0. Therefore, there is a possibility that most neurons would just die off if their output turns to 0, and those parts of the neural net would be dead. We can solve this problem by the following iterations of RELU.
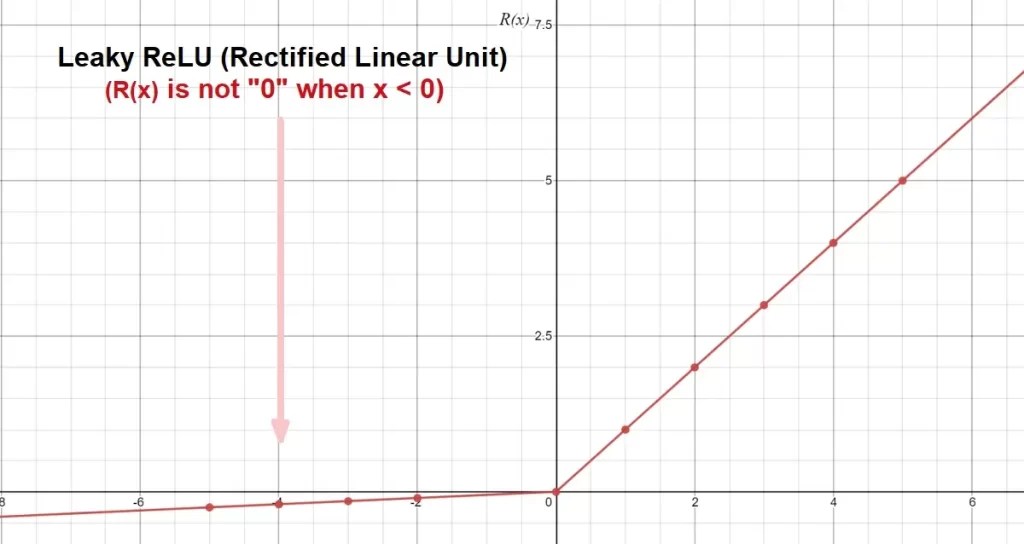
“Leaky ReLU” Activation Function
Leaky ReLU or Leaky Rectified Linear Unit is an improvement on RELU. As we mentioned above, a significant issue of the ReLU activation function is the death of neurons because a negative value turns to “Zero”.
The development of the “Leaky ReLU” was to solve the above issue by replacing the lower straight line with a small slope (leak). The creation of the slope is by multiplying negative numbers by a constant gradient α (Normally, =0.01). We can adjust the variable to suit our needs.
Cons of Leaky ReLU
The value is set to 0.01 and can’t be adjusted over time, and this can become advantageous mainly if 0.01 is not an optimal value.
Pros of Leaky ReLU
- Works better than Sigmoid and ReLU in some cases
- Fast to calculate compared to Sigmoid and Tanh
- Solves the problem of dying nodes with the slope.
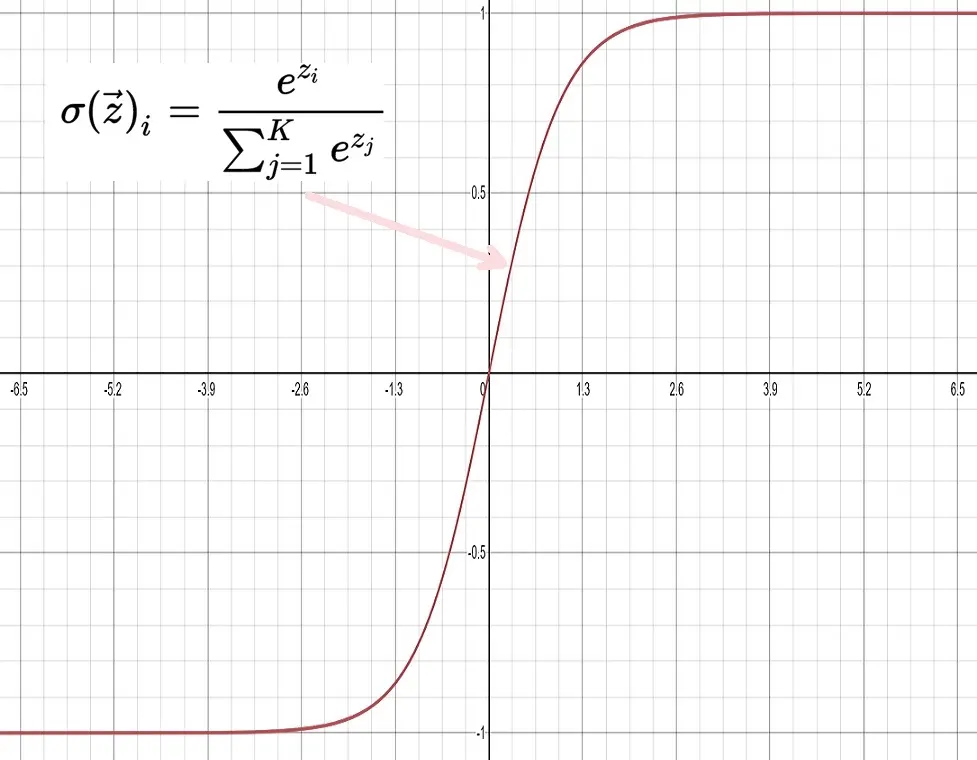
Softmax Activation Function
A softmax function is a very different activation function from the rest because it deals with probability. It is the probability distribution over an N number of classes.
Let’s say we want a machine learning model to predict what number an image passed into it, and we can apply a softmax activation function to the end of the network. This would return a probability distribution that adds up to 1. We usually apply this to the end of the neural network where we want it to calculate probability.
Each output node is defined as a class, and an example would be a network to predict an image of the number 7 passed into it.
The class identified by 7 would have the highest value among other classes. The sum of all classes should equal 1.
Why do we need an activation function for
The purpose of an activation function is to add some non-linearity to the output of a neural network. Without the activation functions, the neural network could perform only linear mappings from inputs “x” to the outputs “y”.
Why is this?
A neural net without an activation function would not be able to realize complex or nonlinear mappings or relationships in data and would be useless in solving complex nonlinear problems.
Without the activation function, we would just have a series of dot-products between input vectors and weights of a matrix.
To perform complex tasks or predictions, neural networks must be able to approximate nonlinear relationships in data, and neural networks without this would not be able to solve tasks that have complex data.
How to choose an activation function?
Choosing an activation function for the hidden layer determines how well our neural network trains from the input data, but the activation function we use for our output function determines the output. Sometimes, activation functions have a range of values for their outputs.
This is called a squashing function. An example would be Tanh and Sigmoid. Hidden layers usually have similar activation functions, but the input and output layers can be different.
The output layer may differ when We want larger numbers above 1, and our hidden networks have sigmoid activation functions. We then use a RELU or leaky RELU activation function for our output node since it isn’t a squash function.
- We want the output of our data to be a distribution of probability that sums up to one, and we can use Softmax;
To choose our activation function, we have to look at the problem we wish to solve, which implies the result from our output node. Following are the simple rules you can easily follow.
- For binary classification (YES/NO): Sigmoid or Softmax.
- For multiclass: Softmax or sigmoid (I would prefer softmax).
- Regression: Any linear function would work.

Somto Achu is a software engineer from the U.K. He has rich years of experience building applications for the web both as a front-end engineer and back-end developer. He also writes articles on what he finds interesting in tech.