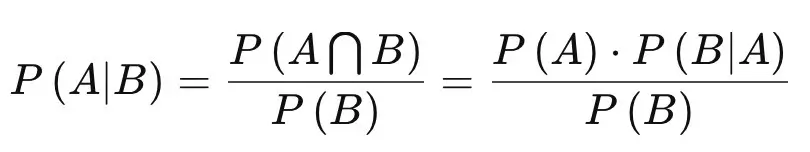An Introduction to Bayesian Network for Machine Learning
A Bayesian network is a graphical model representing probabilistic relationships among variables. This helps in understanding how different factors influence each other and in predicting the behavior of one variable based on the others.
Purposes Served by Bayesian Network
In machine learning, a Bayesian network serves several key purposes:
- Understanding and Visualization: It provides a clear and intuitive visual representation of the dependencies between various variables. This helps researchers and practitioners understand complex relationships and interactions within the data.
- Probabilistic Inference: Bayesian networks are especially useful for making predictions about uncertain events. They allow for probabilistic reasoning, which means you can calculate the likelihood of certain outcomes when some of the variables are known.
- Decision Making: They can be used to model decision processes, incorporating uncertainty and various outcomes to aid in making informed decisions.
- Dealing with Missing Data: Bayesian networks can handle incomplete data sets by making inferences about missing values, which is a common challenge in real-world data.
- Learning from Data: They can be trained with data to learn the relationships between variables, which can then be used to predict future events or conditions.
These capabilities make Bayesian networks a powerful tool in areas such as diagnostics, forecasting, and any domain requiring modeling of complex interactions under uncertainty.
Probabilistic Models and Bayesian Network Vs. Naive Bayes
Probabilistic models are based on the theory of probability. I guess that was quite self-explanatory, considering it is in the name.
Probabilistic models consider the fact that randomness plays a role in predicting future outcomes. The opposite of randomness is deterministic, which tells us that something can be predicted exactly without any underlying randomness.
A Bayesian Network or Bayes network is a decision tree that graphically represents the connection of various variables and their conditional dependencies for predicting the possibilities of an outcome or outcomes.
Bayesian Network models require high amounts of data to cover all possible outcomes. In addition, due to the amount of data, the probabilities may be hard to control and calculate.
Simplifying this process by using a classifier that assumes the independence between attributes of data points is called Naive Bayes. Well-known uses of Naive Bayes classifiers are spam filters, text analysis, and medical diagnosis.
A Naive Bayes classifier is a simple model that describes a particular class of Bayesian network, stating that all the features are class-conditionally independent.
There are specific issues that Naive Bayes cannot solve, which is where the Bayesian Network comes in. However, the simplicity of Naive Bayes makes it easier to apply and requires less data to get efficient outputs.
Naive Bayes and Bayesian Networks come from Bayes’ Theorem. So, let’s get a better understanding of that first.
Bayes’ Theorem
Bayes’ Theorem, also called Bayes’ rule or Bayes’ law, is about the probability of an event, considering the knowledge and conditions that might be associated with the event.
At face value, it looks simply that if we already know that some specific conditions or situations resulted in some specific outcome, then the same outcome would be more with the same conditions and situations repeating. However, it’s not simple, as conditions may be similar but never the same.
Bayes’ Theorem gets its name from English statistician Thomas Bayes. For example, getting affected by a virus during a pandemic is more likely if we live in more densely populated cities or areas. This is logical also, and the past might have proved it.
However, Bayes’ Theorem connects population density with the probability of getting infected, but it also tries to make a more accurate estimate of the risk for a person living in a specific area. It does it by eliminating the assumption that the person represents the whole population of that city or area.
Let’s break it down. Baye’s Theorem is a mathematical formula to determine conditional probability. Conditional probability is the possibility of an outcome occurring based on previous ones.
We use Bayes’ Theorem to provide outputs on new or additional data by examining existing outcomes. For example, we can implement Bayes’ Theorem to rate the risk of lending money to potential borrowers in the finance sector.
Bayes’ Theorem Formula:
- P(A) = The probability of A occurring
- P(B) = The probability of B occurring
- P(A|B) =The probability of A given B
- P(B|A) = The probability of B given A
- P(A⋂B) = The probability of both A and B occurring
What is a Bayesian Network?
Bayesian Networks are probabilistic graphical models that we implement with the Bayesian inference for probability computations. A Bayesian Network aims to develop a model that maintains known conditional dependence between random variables and conditional independence in all other cases.
Using data and experts ‘ opinions, we can build a Bayesian Network for building models. It consists of two parts:
- Directed Acyclic Graph
- Table of conditional probabilities.
The Bayesian Network is a useful tool. It visualizes the probabilistic model and reviews the relationships between the random variables, allowing one to infer the random variables in the graph. They can be used for tasks such as prediction, anomaly detection, automated insight, time series prediction, and decision-making under uncertainty.
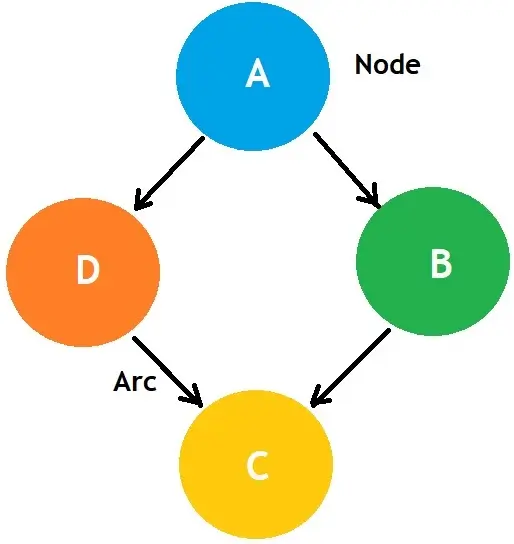
A Bayesian network graph comprises nodes and arcs (edges).
A node represents random variables, which can be continuous or discrete. An arc represents a relationship or conditional probabilities between random variables.
- The arcs show a link between one node and its influence on another.
- If there is a link between the nodes, the nodes are independent.
How to Use a Bayesian Network?
To develop a Bayesian Network, you must define three elements: Random Variables, Conditional Relationships, and Probability Distribution.
- What are the random variables in the problem?
- What are the conditional relationships between the variables?
- What are the probability distributions for each variable?
An Example of a Bayesian Network
I will go through an example while covering the first two questions above.
1. What are the random variables in the problem?
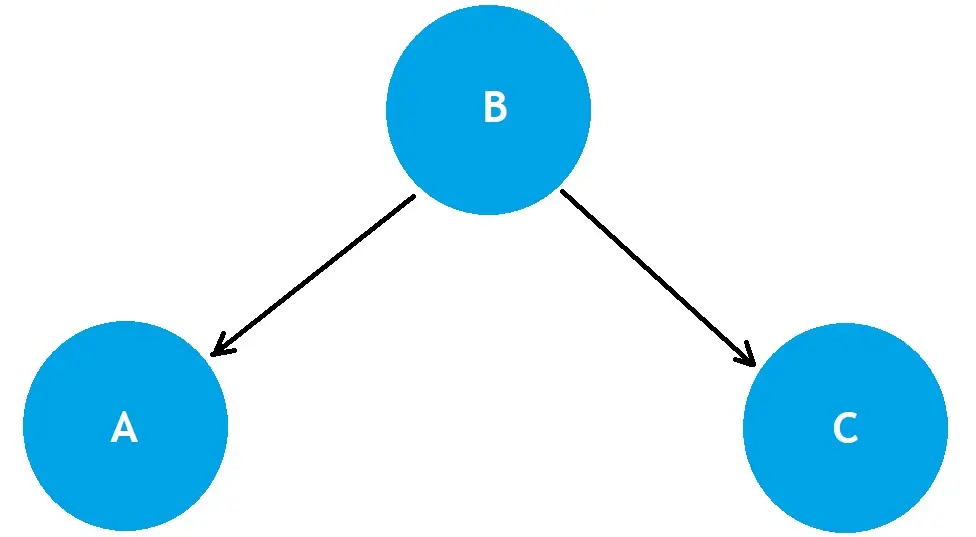
Let’s say we had three random variables: A, B, and C. A is dependent upon B, and C is dependent upon B.
2. What are the conditional relationships between the variables?
We can, therefore, state that the conditional dependent relationship between the variables is:
- A is conditionally dependent on B: P(A|B)
- C is conditionally dependent on B: P(C|B)
Understanding the random variables and the conditional relationships between them allows us to identify the conditionally independent relationships. Since C and A do not affect one another, we can state the conditional independence as:
- A is conditionally independent of C given B: P(A|B, C) = P(A|B)
- C is conditionally independent of A given B: P(C|B, A) = P(C|B)
The above equations represent that the probability of A does not change with knowledge of C once B is known, and similarly for C with respect to A.
For variable B, which has no parents and is independent of A or C, its marginal probability is simply P(B). Therefore, we can express the joint probability of A and C given B as:
P(A, C | B) = P(A|B) * P(C|B)
This follows from the assumption of conditional independence between A and C given B. Finally, the summary of the joint probability of A, B, and C is as follows:
P(A, B, C) = P(A|B) * P(C|B) * P(B)
This is because we multiply the conditional probabilities of A and C given B by the marginal probability of B.
This explanation assumes a Bayesian network where B influences A and C, and A and C are conditionally independent of each other given B.
Diagram to Explain Conditional Relationships
The following diagram summarizes the above conditional relationships of A, B, and C:
This diagram shows that each variable is assigned as a Node, which is correct as they all represent a random variable.
The arcs represent a link between one node and its influence on another. For example, we know that A and C do not influence one another; therefore, there is no arc. However, B has a relationship with both A and C.
Conclusion
To understand the semantics of the Bayesian network, you need to understand the following:
- Construct the network: Understand the network as the representation of the Joint probability distribution.
- Designing Inference Procedure: Understand the network to encode a collection of conditional independence statements.
In conclusion, Bayesian networks provide a powerful framework for understanding the probabilistic relationships between various variables in a complex system. By representing variables as nodes and their conditional dependencies as directed edges, these networks allow us to visualize and compute the intricate web of interactions that influence outcomes.
Through this article, we have explored the foundational concepts of conditional dependence and independence, crucial for efficiently computing probabilities in Bayesian networks. We’ve seen that conditional independence simplifies the overall structure of the network, reducing computational complexity by allowing us to focus only on the direct dependencies.
The principle that variables A and C are conditionally independent given B (P(A|B, C) = P(A|B) and P(C|B, A) = P(C|B)) enables us to compute the joint probability of multiple variables with less information than would otherwise be required. This aspect is particularly advantageous in real-world applications where data may be scarce or expensive.
The calculation of joint probabilities, such as P(A, B, C) = P(A|B) * P(C|B) * P(B), illustrates the practical use of Bayesian networks in determining the likelihood of combined events, which is essential in fields ranging from machine learning to medical diagnosis.
Overall, Bayesian networks embody the essence of probabilistic reasoning, allowing us to make informed predictions and decisions under uncertainty. As our understanding of these networks deepens, so does our ability to model complex phenomena, extract meaningful insights from data, and contribute to advancements across many scientific and technological domains.
Bayesian Network Software
- JAGS (Just Another Gibbs Sampler): Open-source (download JAGS)
- MultiBUGS: A software package for performing Bayesian inference. It builds on the existing algorithms and tools in OpenBUGS and WinBUGS – Open-source.
- SPSS Modeler: Commercial software from IBM
- Stan: Open-source
- PyMC (formerly PyMC3): A Python library (PyMC GitHub)
- BNLearn: An R package for learning the graphical structure of Bayesian networks

Nisha Arya is a Data Scientist and Technical writer from London.
Having worked in the world of Data Science, she is particularly interested in providing Data Science career advice or tutorials and theory-based knowledge around Data Science. She is a keen learner seeking to broaden her tech knowledge and writing skills while helping guide others.