Guide to Cross-validation in Machine Learning

Cross-validation is a technique used in machine learning to assess how well a model will generalize to an independent data set.

What is Cross-Validation?

Imagine you’re a teacher preparing a test for your students. You want to ensure that the test accurately reflects how well your students understand the material and not just how well they memorized specific questions you used during their revision.

So, you might create several test versions and have each student take a few of them. This way, you can be more confident that the students’ scores reflect their true understanding, not just their memory of specific questions.

Cross-validation in machine learning is a bit like that. When we build a model (think of it as a student) using a dataset (the study material), we want to ensure that our model performs well not just on the data it was trained on but also on new, unseen data. Cross-validation helps us do that.

What Cross-Validation Involves?

Cross-validation involves dividing the available data into parts, usually termed ‘folds’, and then systematically training and evaluating the model multiple times, each time with a different fold held out for testing.

The process of cross-validation helps ensure that the model’s performance is consistent across different subsets of data and not just tailored to one specific set. By averaging the model’s performances across all iterations, we get a more accurate measure of its ability to predict new, unseen data.

You may have heard the term ‘generalization’ used when speaking or hearing about Machine Learning. Generalization refers to the algorithm’s capabilities to work effectively across various inputs. This means that it performs well on new inputs with the same characteristics or similarities in the data points in the training data. 

However, being able to detect new inputs can be a challenge for Machine Learning models. We can easily generalize things, and it’s second nature to us. Therefore, checking that algorithms have a high ability to generalize is a crucial element. To achieve this, we use Cross-Validation.

Cross Validation in Machine Learning

Cross-validation is also known as rotation estimation and/or out-of-sample testing. It evaluates how well the statistical analysis results can generalize to unseen data.

Cross-validation is very popular due to its simple understanding and easy implementation, and it generally has a lower bias than other methods. 

There are different types of Cross-Validation techniques. Here are a few which I will go into deeper:

• Hold-out
• K-folds
• Leave-one-out
• Leave-p-out

Cross-Validation Process

Following is a simple breakdown of the cross-validation process:

1. Splitting the Data:

We divide our data into two parts: training data and testing data. Training data is like the revision material, and testing data is like the exam questions. Often, we split the data into even more parts to run several rounds of training and testing.

2. Training the Model:

The model learns from the training data. It tries to understand the patterns or relationships within it, much like how students understand the course material during revision.

3. Testing the Model:

We then test the model using the testing data to see how well it can predict new, unseen information. This is akin to giving our students a test on their studied material to see how well they’ve understood it.

4. Assessing the Model:

By looking at how well the model performed on the testing data (how accurately it made predictions), we get an idea of how well it has “learned” the patterns in the data. If a student scores well on the test, it indicates they’ve understood the material.

5. Repeat:

In cross-validation, we don’t just do this process once. We repeat it multiple times with different parts of the data used for training and testing. This is like making students take several test versions to ensure their knowledge is solid.

6. Average the Results:

Finally, we take the average of all these tests to estimate better how well the model performs, just like taking an average of all the test scores from our students gives us a better understanding of their overall knowledge.

Cross-validation helps us ensure that our machine-learning model is robust and reliable by testing it in multiple ways before we put it into practice. It’s a crucial step in ensuring that our models will perform well, not just on our existing data but on new, unseen data in the future!

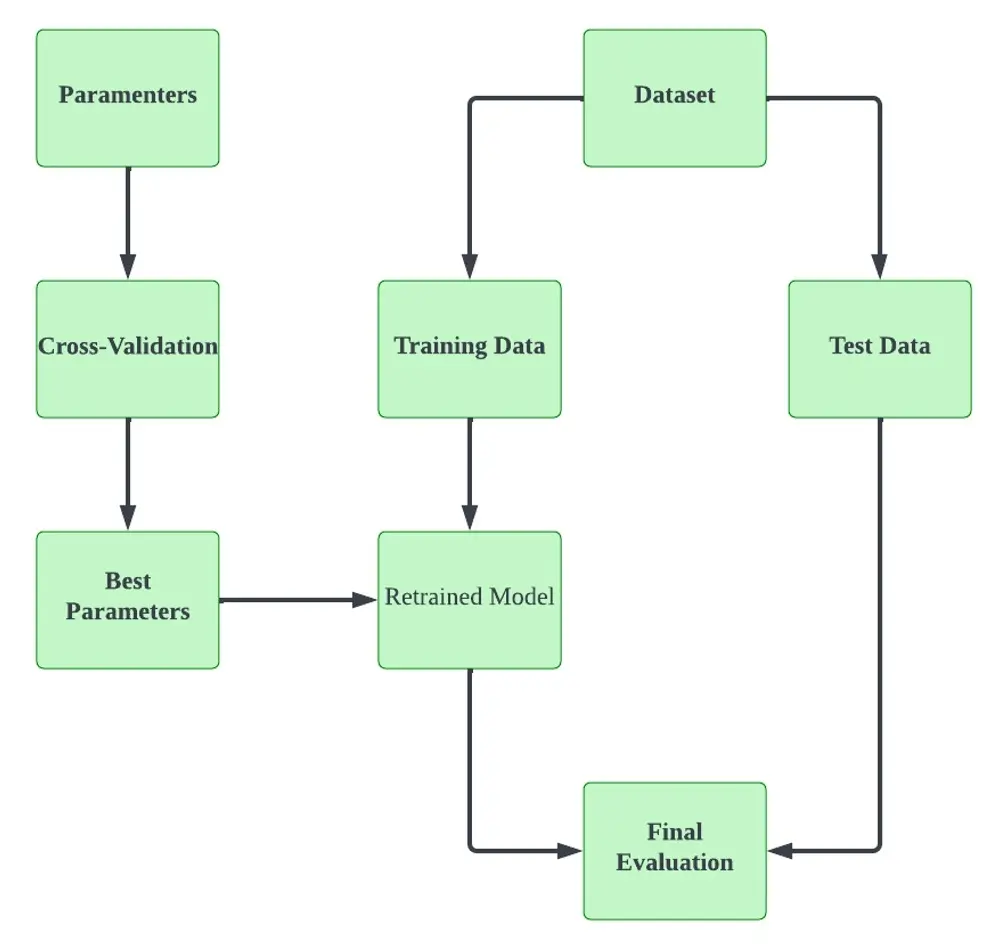
Cross-Validation Workflow

Below is a typical Cross-Validation workflow diagram. The dataset will be split into training data and test data. The parameters will undergo Cross-Validation, which will select the best parameters. This will then be fed into the model to be retrained to improve the overall performance and accuracy of the model.

Hold-out Cross-Validation

The hold-out cross-validation method is one of the simplest and most common techniques. It separates the data set into two sets – the training set and the testing set. 

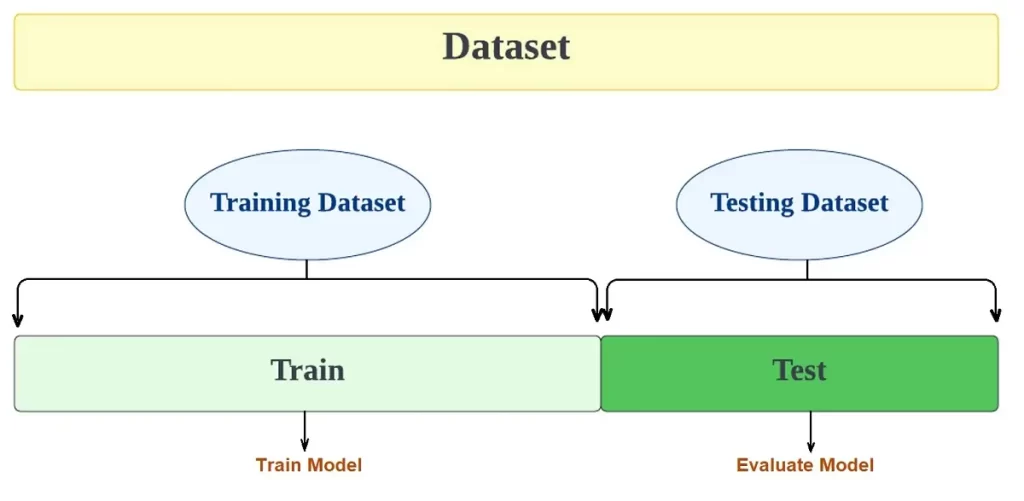
The model learns from the training data set and then is asked to make predictions on the testing dataset. The model has not seen the values for the training dataset before. The mean absolute error produced on the test dataset will be used to evaluate the model.

The steps for Hold-out Cross-Validation

1. Divide the dataset into the training set and the test set. This is usually 80% for the training set and 20% for the test set.
2. Train the model on the training dataset
3. Validate the model on the test dataset
4. Save the result of the validation (mean absolute error)

You can easily implement this using “sklearn.model_selection.train_test_split”. Following is the code for Hold-out Cross-Validation:

import numpy as np
from sklearn.model_selection import train_test_split

X, y = np.arange(10).reshape((5, 2)), range(5)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=111)

K-fold Cross-Validation

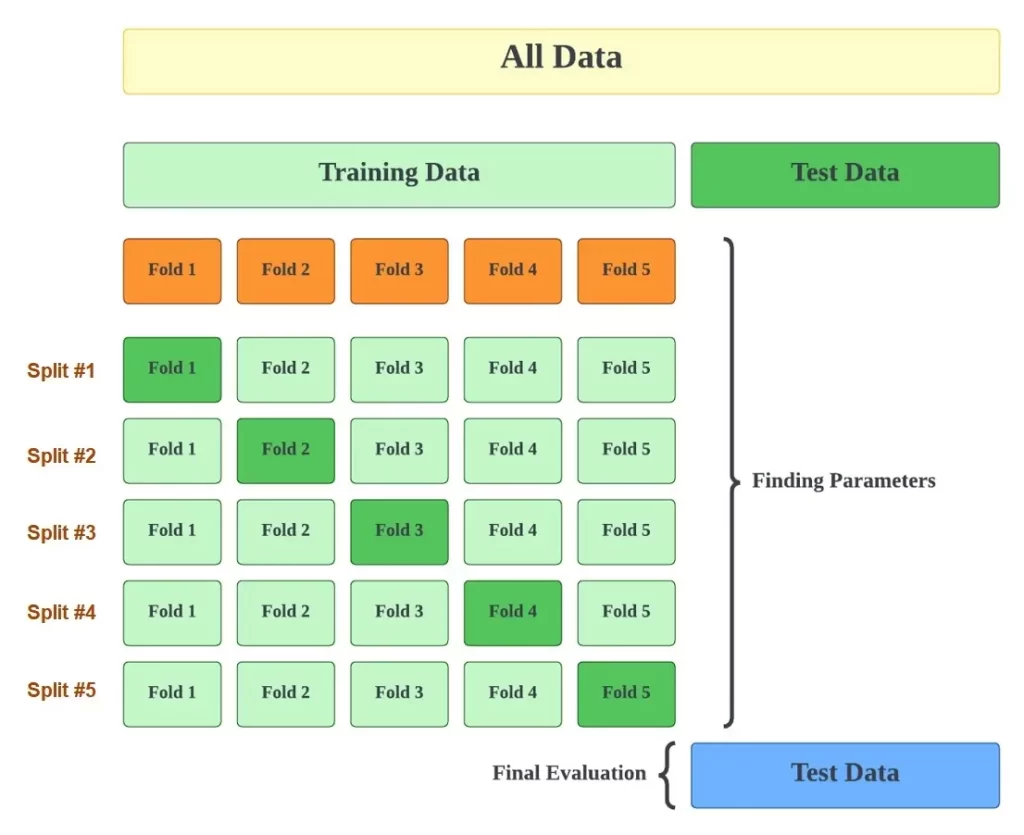
K-fold Cross-Validation refers to when a data set is split into a K-number of folds. K is a single parameter that refers to the number of groups the data sample is split into. Using a k-value of 7, we can call this a 7-fold cross-validation.

Each of these folds is used as a testing set at some point. This procedure is to evaluate the model’s ability when given new data.

How do you choose the k-value?

If you don’t choose the k-value correctly, it can lead to high variance, which may be due to the misrepresentative skill of the model. On the other hand, it can also lead to a high bias, which may be due to the overestimated skill of the model. 

In order to choose the right k-value, these are some methods you can use:

1. k=n: n represents the size of the dataset, allowing each test sample to be used in the test data or hold-out data. This is also known as leave-one-out cross-validation, which we will explore further. 
2. k=10: Through various experiments, fixing the k-value at 10 has provided a low bias and a modest variance. 

The steps for K-fold Cross-Validation:

1. Choose your k-value (the number of folds). 
2. Split the dataset into several k folds.
3. Use the k 1-fold as the training dataset and the remaining folds as a test dataset.
4. Train the model on the training dataset.
5. Validate on the test dataset.
6. Save the result of the validation.
7. Repeat steps 3 – 6, depending on your chosen k-value. For example, if you chose k=10, you will repeat the step another 9 times. 
8. Each time, you will use the remaining fold previously used as the training dataset as the test dataset. In the end, you should have validated the model on every fold.
9. You would have validated the model on every fold. Therefore, to get the final score, you average the results produced in step 6.

You can easily implement this using “sklearn.model_selection.KFold”. Please check the following code for K-fold Cross-Validation:

import numpy as np
from sklearn.model_selection import KFold

X = np.array([[1, 2], [3, 4], [1, 2], [3, 4]])
y = np.array([1, 2, 3, 4])
kf = KFold(n_splits=2)

for train_index, test_index in kf.split(X):
    print("TRAIN:", train_index, "TEST:", test_index)
    X_train, X_test = X[train_index], X[test_index]
    y_train, y_test = y[train_index], y[test_index]

Leave-one-out Cross-Validation

Leave-one-out cross-validation (LOOCV) is a branch of K-fold cross-validation, just an exhaustive form. Instead of assigning k to a specific number, we assign it to the number of data points in the set. The model is trained on all the data points except for one point, the test dataset, and the predictions are made from this. 

The steps for Leave-one-out Cross-Validation:

1. Choose one sample from the dataset and assign this as your test dataset.
2. The remaining samples will be your training dataset
3. Train the model on the training set.
4. Validate on the test dataset.
5. Save the result of the validation.
6. Repeat steps 1 – 5 till your n value has been met. 
7. You would have validated the model on every n value. Therefore, you average the results produced in step 4 to get the final score.

You can easily implement this using “sklearn.model_selection.LeaveOneOut”. The following code implements Leave-one-out Cross-Validation:

>>> from sklearn.model_selection import LeaveOneOut

>>> X = [1, 2, 3, 4]
>>> loo = LeaveOneOut()
>>> for train, test in loo.split(X):
...    print("%s %s" % (train, test))
[1 2 3] [0]
[0 2 3] [1]
[0 1 3] [2]
[0 1 2] [3]

Leave-p-out Cross-Validation

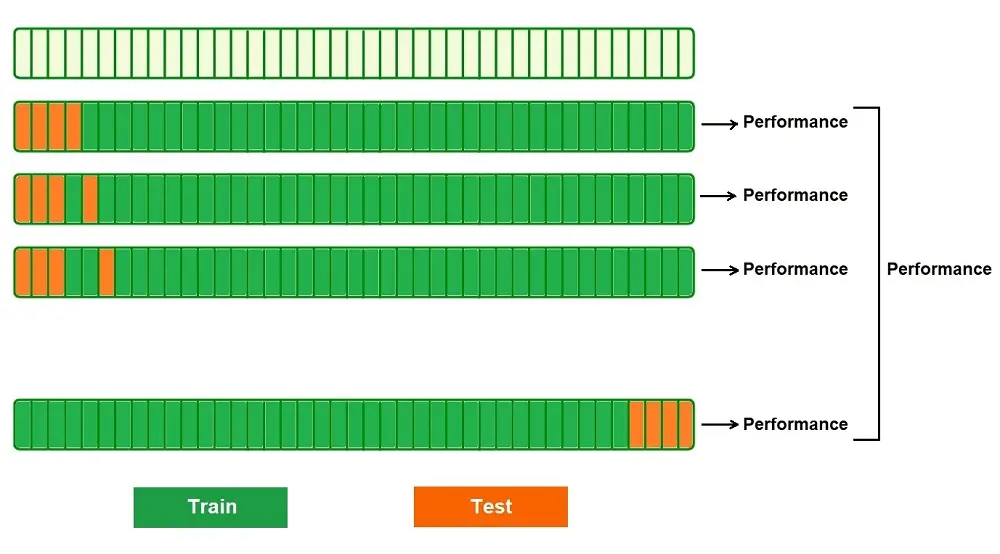
Leave P Out (LPO) is also an exhaustive form of K-fold cross-validation and is very similar to LOOCV. In this method, we take “p” number of points from the total data points in the dataset. The training dataset is calculated by the number of data points – p points (n-p). N-p data points are used for training the model, whereas the p points are used for testing.

All possible combinations of “p” are generated, and the process is repeated to get the final accuracy.

The steps for Leave-p-out Cross-Validation:

1. Select a p sample from the dataset. This will be the test set
2. n – p will be the training set
3. Train the model on the training set. 
4. Validate on the test set
5. Save the result of the validation
6. Repeat steps 2 – 5 till Cpn has been met. Each time, you will be allocating your p-value to different sets.
7. You would have validated the model on every CPN. Therefore, to get the final score, you average the results that were produced in step 5.

You can easily implement this using sklearn.model_selection.LeavePOut. Following is the code for Leave-p-out Cross-Validation:

>>> from sklearn.model_selection import LeavePOut
>>> X = np.ones(4)
>>> lpo = LeavePOut(p=2)
>>> for train, test in lpo.split(X):
...    print("%s %s" % (train, test))
[2 3] [0 1]
[1 3] [0 2]
[1 2] [0 3]
[0 3] [1 2]
[0 2] [1 3]
[0 1] [2 3]

Conclusion

Cross-validation is an important tool that every Data Scientist should be using. More Cross-Validation techniques are very common, such as: 

• Stratified K-folds
• Repeated K-folds
• Nested K-folds
• Time-series CV

If you would like to know more about these, check out sci-kit learn.

Nisha Arya

Nisha Arya is a Data Scientist and Technical writer from London. 

Having worked in the world of Data Science, she is particularly interested in providing Data Science career advice or tutorials and theory-based knowledge around Data Science. She is a keen learner seeking to broaden her tech knowledge and writing skills while helping guide others.